Session 2 : Describing Syntax and Semantics

On this session, i just write about the meaning of syntax and semantics and some grammar from concept of programming language by Robert W Sebesta.
Syntax => the form or structure of the expressions statements, and program units.

Semantics => is the meaning of the expressions, statements, and program units.

Syntax ans semantics provide a language's definitions :
  Users of a language designers :
    -Other Language designers.
    -Implementers.
    -Programmers (the users of the language).

A Grammar for a Small Language
<program> → begin <stmt_list> end
<stmt_list> → <stmt>
     | <stmt> ; <stmt_list>
<stmt> → <var> = <expression>
<var> → A | B | C
<expression> → <var> + <var>
      | <var> – <var>
      | <var>

Derivation of a program
example :
A = B * ( A + C )
is generated by the leftmost derivation:
<program> => begin <stmt_list> end
  => begin <stmt> ; <stmt_list> end
  => begin <var> = <expression> ; <stmt_list> end
          => begin A = <expression> ; <stmt_list> end
  => begin A = <var> + <var> ; <stmt_list> end
  => begin A = B + <var> ; <stmt_list> end
  => begin A = B + C ; <stmt_list> end
  => begin A = B + C ; <stmt> end
  => begin A = B + C ; <var> = <expression> end
  => begin A = B + C ; B = <expression> end
  => begin A = B + C ; B = <var> end
  => begin A = B + C ; B = C end

A Grammar for Simple Assignment Statements
<assign> → <id> = <expr>
<id> → A | B | C
<expr> → <id> + <expr>
| <id> * <expr>
| ( <expr> )
| <id>
for example :
A = B * ( A + C )
is generated by the leftmost derivation:
<assign> => <id> = <expr>
=> A = <expr>
=> A = <id> * <expr>
=> A = B * <expr>
  => A = B * ( <expr> )
=> A = B * ( <id> + <expr> )
=> A = B * ( A + <expr> )
=> A = B * ( A + <id> )
=> A = B * ( A + C )

Parse tree
One of the most attractive features of grammars is that they naturally describethe hierarchical syntactic structure of the sentences of the languages they define. These hierarchical structures are called parse trees.
example :

Ambiguity => A grammar that generates a sentential form for which there are two or more distinct parse trees is said to be ambiguous
An Ambiguous Grammar for Simple Assignment Statements
<assign> → <id> = <expr>
<id> → A | B | C
<expr> → <expr> + <expr>
| <expr> * <expr>
| ( <expr> )
| <id>

An Unambiguous Grammar for Expressions
<assign> → <id> = <expr>
<id> → A | B | C
<expr> → <expr> + <term>
| <term>
<term> → <term> * <factor>
| <factor>
<factor> → ( <expr> )
| <id>
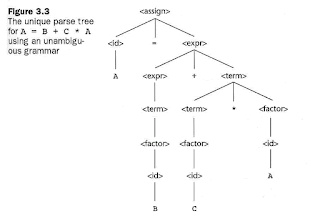
example :
A = B + C * A
uses that an ambigous grammar,
<assign> => <id> = <expr>
=> A = <expr>
=> A = <expr> + <term>
=> A = <term> + <term>
=> A = <factor> + <term>
=> A = <id> + <term>
=> A = B + <term>
=> A = B + <term> * <factor>
=> A = B + <factor> * <factor>
=> A = B + <id> * <factor>
=> A = B + C * <factor>
=> A = B + C * <id>
=> A = B + C * A

BNF and EBNF Versions of an Expression Grammar
BNF:
<expr> → <expr> + <term>
| <expr> - <term>
| <term>
<term> → <term> * <factor>
| <term> / <factor>
| <factor>
<factor> → <exp> ** <factor>
   <exp>
<exp> → (<expr>)
| id
EBNF:
<expr> → <term> {(+ | -) <term>}
<term> → <factor> {(* | /) <factor>}
<factor> → <exp> { ** <exp>}
<exp> → (<expr>)
| id
BNF rule
An abstraction (or nonterminal symbol) can have more than one RHS
     <stmt> → <single_stmt>
             | begin <stmt_list> end